Adrian A. Drăgulescu
October 3, 2025
Introduction
The New York Times launched a new puzzle game called Pips on August 18, 2025. To solve the puzzle, the player needs to place dominoes on a board in a way that satisfies a set of constraints. It comes in 3 flavors (small, medium and hard) based on the size of the board. The board shape and the constraints are different every day.
Here's the easy puzzle from September 16, 2025:
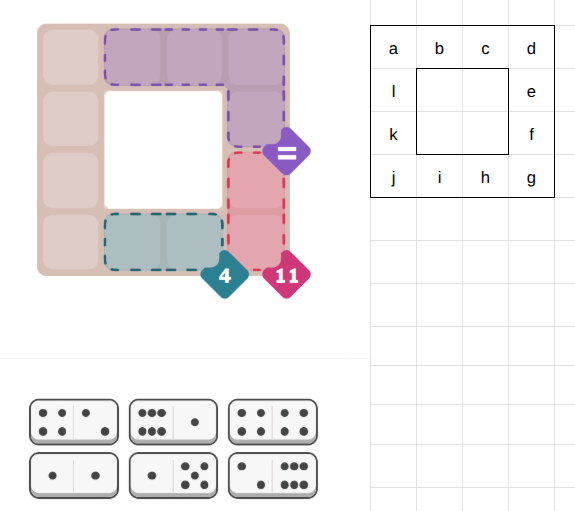
In this puzzle, there are 6 dominoes to fill a 12 square grid and three constraints on the dominoes values (pips). To facilitate the discussion, I've labeled the squares from a to l as shown on the right. The constraints require that
b = c = d = e
f + g = 11
h + i = 4
A naive way to solve the puzzle is to generate all the possible domino arrangements that fill
the board and check which one satisfies the given constraints. For this puzzle, given that there
are 6 dominoes, there are 6! ways of placing them on the grid. However, each domino can be
flipped so there are 2^6 ways to do that. In total, there are 2^6 * 6! = 46,080 arrangements
to check, which can be checked easily by computer.
Hard puzzles have 12 dominoes or more. For a puzzle with 12 dominoes, there are
2^12 * 12! = 1,961,990,553,600 possible arrangements. In this case the naive, brute force approach
is unfeasible.
It's time for the Constraint Programming solver to enter the chat...
Solution
To solve the puzzle we need to decompose the problem into two parts. First, find all the
distinct ways to lay the dominoes on the grid and then second, satisfy the constraints. In
the following, we'll refer to the first problem as the link problem, and the latter
as the value problem. Both problems will be solved by constraint programming, in particular
by a SAT solver. For the implementation,
I'll use the Python package from the excellent Google OR-Tools solver but many other SAT solvers are available.
For the puzzle presented in the previous section there are exactly two ways
in which dominoes can be arranged on the grid. If we denote the link between
two nodes a and b as (a-b), the only two possible layouts for the previous
puzzle are
['(a-b)', '(c-d)', '(e-f)', '(g-h)', '(i-j)', '(k-l)']
['(a-l)', '(b-c)', '(d-e)', '(f-g)', '(h-i)', '(j-k)']
The two layouts are determined by wether the domino containing the node a is placed
horizontally or vertically. Once that decision is made, the position of all
the other dominoes is determined. In general, for more complicated puzzles with a
higher connectivity between nodes, there can be hundreds of possible layouts.
To model a puzzle, we label all the nodes, describe the links between the nodes, and the puzzle constraints. Here is our description for the puzzle from the previous section
puzzle = {
"dominoes": {(2, 4), (1, 6), (4, 4), (1, 1), (1, 5), (2, 6)},
"constraints": [
ConstraintEqual(["b", "c", "d", "e"]),
ConstraintSum(["f", "g"], 11),
ConstraintSum(["h", "i"], 4),
],
"links": {
"a": ["b", "l"],
"b": ["a", "c"],
"c": ["b", "d"],
"d": ["c", "e"],
"e": ["d", "f"],
"f": ["e", "g"],
"g": ["f", "h"],
"h": ["g", "i"],
"i": ["h", "j"],
"j": ["i", "k"],
"k": ["j", "l"],
"l": ["k", "a"],
},
}
Each constraint type is modeled as a Python class. All constraint classes implement the
method is_satisfied(self, cells: Dict[str, int]).
Note how the values of the links dict are lists of nodes with one or more elements. All
nodes need to appear in this dict.
A solution to the puzzle needs to specify both the values of pips at each node and how the dominoes are placed (which two nodes make a domino). For our puzzle, the solution is
{
"values": [6, 1, 1, 1, 1, 5, 6, 2, 2, 4, 4, 4],
"config": [
"(a-b)",
"(c-d)",
"(e-f)",
"(f-g)",
"(h-i)",
"(j-k)",
"(k-l)",
],
},
Solving the link problem
To translate the link problem into a SAT formulation, we model each link between two nodes as a boolean variable. When the value of the variable equals 0, the two nodes are not linked, and when it equals 1, the two nodes are linked. The model has the constraints that a node can only be linked to another node.
Start by creating the constraint propagation model model = CpModel().
Create the variables for the link problem
x: List[IntVar] = []
for cell, neighbors in puzzle["links"].items():
for neighbor in neighbors:
if cell < neighbor: # to avoid duplicates
x.append(model.new_int_var(0, 1, f"({cell}-{neighbor})"))
then impose the constraint that a node is only linked to another node.
for cell, neighbors in puzzle["links"].items():
model.add(
sum(
[
x[i]
for i in range(N)
if x[i].name
in [
f"({cell}-{n})" if cell < n else f"({n}-{cell})"
for n in neighbors
]
]
)
== 1
)
Then solve the model, by requesting all solutions.
solver = CpSolver()
solver.parameters.enumerate_all_solutions = True
solution_printer = PipsLinksSolutionPrinter(x)
status = solver.solve(model, solution_printer)
if status != cp_model.OPTIMAL:
print("Not all link solutions were found!")
For our easy puzzle, there will be only two solutions returned as mentioned above.
Solving the value problem
To solve the value problem as a SAT, we model each node as seven boolean variables
corresponding to values 0 to 6. Our puzzle with 12 nodes has 84 variables.
nodes = list(puzzle["links"].keys())
# define the model variables
x: List[IntVar] = []
for i in range(len(nodes) * 7):
x.append(model.new_int_var(0, 1, f"{nodes[i // 7]}_{i % 7}"))
And impose the constraint that only one of the seven variables is true for each node; that is each node takes only one value.
for i in range(N):
model.add(sum(x[i * 7 + j] for j in range(7)) == 1)
We then impose the puzzle constraints. For simplicity, we'll write them non-generic, for our specific puzzle
model.add(x[7 + i] == x[14 + i] for i in range(7)) # b = c
model.add(x[7 + i] == x[21 + i] for i in range(7)) # b = d
model.add(x[7 + i] == x[28 + i] for i in range(7)) # b = e
model.add(i*sum(x[35 + i] for i in range(7)) + i*sum(x[42 + i] for i in range(7)) == 11) # f + g = 11
model.add(i*sum(x[49 + i] for i in range(7)) + i*sum(x[56 + i] for i in range(7)) == 4) # h + i = 4
To restrict the model further, we use the dominoes values. We add an additional set of constraints that limit the number of variables of a given value to how many times that value appears in the dominoes. For example, there are no zeros in the dominoes, there are four ones, etc.
# Impose the constraints from the domino counts
counts = {n: sum(t.count(n) for t in puzzle["dominoes"]) for n in range(7)}
for n in range(7):
model.add(sum(x[7 * j + n] for j in range(N)) == counts[n])
This value model by itself, does not solve the puzzle because it will generate solutions that won't satisfy the adjacency constraints imposed by the dominoes. Only when combined with the solutions from the previous link model, you obtain the correct solution to the problem.
In the next section, we'll round up the discussion with a hard puzzle example.
Final remarks
Let's discuss the hard puzzle from September 21, 2005.
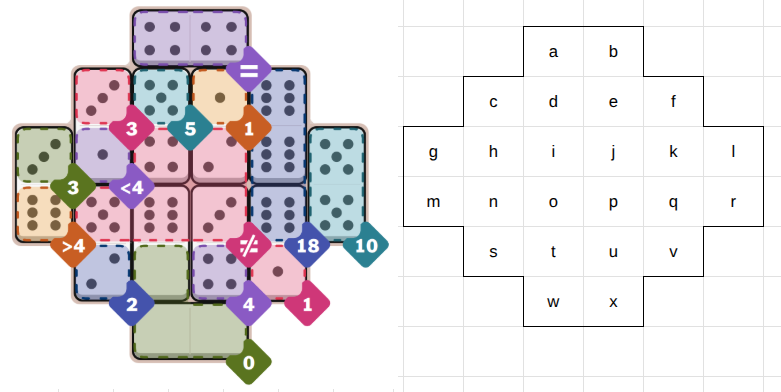
We encode the puzzle as following:
puzzle = {
"dominoes": {
(1, 2),
(0, 6),
(5, 5),
(1, 3),
(4, 4),
(1, 6),
(0, 0),
(3, 4),
(2, 5),
(3, 6),
(6, 6),
(4, 5),
},
"constraints": [
ConstraintEqual(["a", "b"]),
ConstraintSum(["c"], 3),
ConstraintSum(["d"], 5),
ConstraintSum(["e"], 1),
ConstraintSum(["f", "k", "q"], 18),
ConstraintSum(["g"], 3),
ConstraintLessThan(["h"], 4),
ConstraintNotEqual(["i", "j", "n", "o", "p"]),
ConstraintGreaterThan(["m"], 4),
ConstraintSum(["l", "r"], 10),
ConstraintSum(["s"], 2),
ConstraintSum(["t", "w", "x"], 0),
ConstraintSum(["u"], 4),
ConstraintSum(["v"], 1),
],
"links": {
"a": ["b", "d"],
"b": ["a", "e"],
"c": ["d", "h"],
"d": ["a", "c", "e", "i"],
"e": ["b", "d", "f", "j"],
"f": ["e", "k"],
"g": ["h", "m"],
"h": ["c", "g", "i", "n"],
"i": ["d", "h", "j", "o"],
"j": ["e", "i", "k", "p"],
"k": ["f", "j", "l", "q"],
"l": ["k", "r"],
"m": ["g", "n"],
"n": ["h", "m", "o", "s"],
"o": ["i", "n", "p", "t"],
"p": ["j", "o", "q", "u"],
"q": ["k", "p", "r", "v"],
"r": ["l", "q"],
"s": ["n", "t"],
"t": ["o", "s", "u", "w"],
"u": ["p", "t", "v", "x"],
"v": ["q", "u"],
"w": ["t", "x"],
"x": ["u", "w"],
},
}
One can see that this puzzle has a much higher connectivity than the easy puzzle that was presented in the previous section. There are 64 solutions for the link problem. We show below the first two and the last two solutions
['(a-b)', '(c-d)', '(e-f)', '(g-h)', '(i-o)', '(j-p)', '(k-l)', '(m-n)', '(q-r)', '(s-t)', '(u-v)', '(w-x)']
['(a-b)', '(c-d)', '(e-f)', '(g-m)', '(h-n)', '(i-o)', '(j-p)', '(k-l)', '(q-r)', '(s-t)', '(u-v)', '(w-x)']
...
['(a-d)', '(b-e)', '(c-h)', '(f-k)', '(g-m)', '(i-j)', '(l-r)', '(n-o)', '(p-u)', '(q-v)', '(s-t)', '(w-x)']
['(a-d)', '(b-e)', '(c-h)', '(f-k)', '(g-m)', '(i-j)', '(l-r)', '(n-o)', '(p-q)', '(s-t)', '(u-v)', '(w-x)']
The stand alone value problem results in 360 solutions. That is, we need to check at most
64 * 360 = 23,040 candidates in order to find the true solution. This number is
significantly smaller than the 1,961,990,553,600 candidates needed to be checked if we
had used the brute force approach. But then, who wants to be a brute these days?
In terms of execution time, with the current double SAT modelling, the puzzle is solved in 0.2 seconds, fast enough not be noticeable. You can check out the
code here for a complete implementation. Happy puzzling!