Final remarks

Let's discuss the hard puzzle from September 21, 2005.

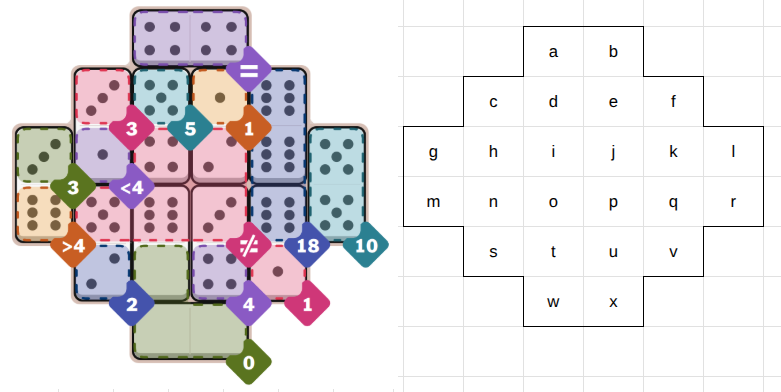
We encode the puzzle as following:

puzzle = {
    "dominoes": {
        (1, 2),
        (0, 6),
        (5, 5),
        (1, 3),
        (4, 4),
        (1, 6),
        (0, 0),
        (3, 4),
        (2, 5),
        (3, 6),
        (6, 6),
        (4, 5),
    },
    "constraints": [
        ConstraintEqual(["a", "b"]),
        ConstraintSum(["c"], 3),
        ConstraintSum(["d"], 5),
        ConstraintSum(["e"], 1),
        ConstraintSum(["f", "k", "q"], 18),
        ConstraintSum(["g"], 3),
        ConstraintLessThan(["h"], 4),
        ConstraintNotEqual(["i", "j", "n", "o", "p"]),
        ConstraintGreaterThan(["m"], 4),
        ConstraintSum(["l", "r"], 10),
        ConstraintSum(["s"], 2),
        ConstraintSum(["t", "w", "x"], 0),
        ConstraintSum(["u"], 4),
        ConstraintSum(["v"], 1),
    ],
    "links": {
        "a": ["b", "d"],
        "b": ["a", "e"],
        "c": ["d", "h"],
        "d": ["a", "c", "e", "i"],
        "e": ["b", "d", "f", "j"],
        "f": ["e", "k"],
        "g": ["h", "m"],
        "h": ["c", "g", "i", "n"],
        "i": ["d", "h", "j", "o"],
        "j": ["e", "i", "k", "p"],
        "k": ["f", "j", "l", "q"],
        "l": ["k", "r"],
        "m": ["g", "n"],
        "n": ["h", "m", "o", "s"],
        "o": ["i", "n", "p", "t"],
        "p": ["j", "o", "q", "u"],
        "q": ["k", "p", "r", "v"],
        "r": ["l", "q"],
        "s": ["n", "t"],
        "t": ["o", "s", "u", "w"],
        "u": ["p", "t", "v", "x"],
        "v": ["q", "u"],
        "w": ["t", "x"],
        "x": ["u", "w"],
    },
}

One can see that this puzzle has a much higher connectivity than the easy puzzle that was presented in the previous section. There are 64 solutions for the link problem. We show below the first two and the last two solutions

['(a-b)', '(c-d)', '(e-f)', '(g-h)', '(i-o)', '(j-p)', '(k-l)', '(m-n)', '(q-r)', '(s-t)', '(u-v)', '(w-x)']
['(a-b)', '(c-d)', '(e-f)', '(g-m)', '(h-n)', '(i-o)', '(j-p)', '(k-l)', '(q-r)', '(s-t)', '(u-v)', '(w-x)']
...
['(a-d)', '(b-e)', '(c-h)', '(f-k)', '(g-m)', '(i-j)', '(l-r)', '(n-o)', '(p-u)', '(q-v)', '(s-t)', '(w-x)']
['(a-d)', '(b-e)', '(c-h)', '(f-k)', '(g-m)', '(i-j)', '(l-r)', '(n-o)', '(p-q)', '(s-t)', '(u-v)', '(w-x)']

The stand alone value problem results in 360 solutions. That is, we need to check at most 64 * 360 = 23,040 candidates in order to find the true solution. This number is significantly smaller than the 1,961,990,553,600 candidates needed to be checked if we had used the brute force approach. But then, who wants to be a brute these days?

In terms of execution time, with the current double SAT modelling, the puzzle is solved in 0.2 seconds, fast enough not be noticeable. You can check out the code here for a complete implementation. Happy puzzling!